HIPERBOLAS
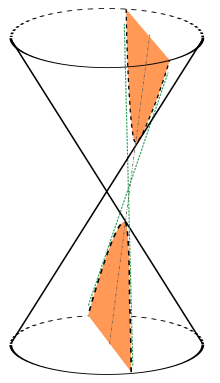
Una hipérbola (del griego ὑπερβολή) es una sección cónica, una curva abierta de dos ramas obtenida al cortar un cono recto por un plano oblicuo al eje de simetría con ángulo menor que el de la generatriz respecto del eje de revolución.[1]Una hipérbola es el lugar geométrico de los puntos de un plano tales que el valor absoluto de la diferencia de sus distancias a dos puntos fijos, llamados focos, es igual a la distancia entre los vértices, la cual es una constante positiva.
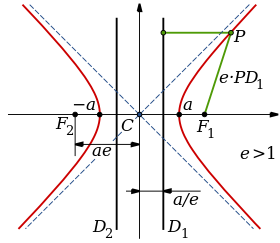
Las asíntotas de la hipérbola se muestran como líneas discontinuas azules que se cortan en el centro de la hipérbola (curvas rojas), C. Los dos puntos focales se denominan F1 y F2, la línea negra que los une es el eje transversal. La delgada línea perpendicular en negro que pasa por el centro es el eje conjugado. Las dos líneas gruesas en negro paralelas al eje conjugado (por lo tanto, perpendicular al eje transversal) son las dos directrices, D1 y D2. La excentricidad e (e>1), es igual al cociente entre las distancias (en verde) desde un punto P de la hipérbola a uno de los focos y su correspondiente directriz. Los dos vértices se encuentran en el eje transversal a una distancia ±a con respecto al centro.
Ecuaciones de la hipérbola Ecuaciones en coordenadas cartesianas: Ecuación de una hipérbola con centro en el origen de coordenadas 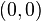 y ecuación de la hipérbola en su forma compleja.
y ecuación de la hipérbola en su forma compleja.

a)
Ecuación de la hipérbola en su forma compleja
Una hipérbola en el plano complejo es el lugar geométrico formado por un conjunto de puntos , en el plano
, en el plano  ; tales que, cualesquiera de ellos satisface la condición geométrica de que el valor absoluto de la diferencia de sus distacias
; tales que, cualesquiera de ellos satisface la condición geométrica de que el valor absoluto de la diferencia de sus distacias 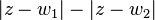 , a dos puntos fijos llamados focos
, a dos puntos fijos llamados focos y
y  , es una costante positiva igual al doble de la distancia (osea
, es una costante positiva igual al doble de la distancia (osea  ) que existe entre su centro y cualesquiera de sus vértices del eje focal.
) que existe entre su centro y cualesquiera de sus vértices del eje focal.
La ecuacion queda:
Evidentemente esta operación se lleva a cabo en el conjunto de los números complejos.
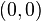 y ecuación de la hipérbola en su forma compleja.
y ecuación de la hipérbola en su forma compleja.
a)
Ecuación de la hipérbola en su forma compleja
Una hipérbola en el plano complejo es el lugar geométrico formado por un conjunto de puntos
 , en el plano
, en el plano  ; tales que, cualesquiera de ellos satisface la condición geométrica de que el valor absoluto de la diferencia de sus distacias
; tales que, cualesquiera de ellos satisface la condición geométrica de que el valor absoluto de la diferencia de sus distacias 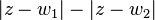 , a dos puntos fijos llamados focos
, a dos puntos fijos llamados focos y
y  , es una costante positiva igual al doble de la distancia (osea
, es una costante positiva igual al doble de la distancia (osea  ) que existe entre su centro y cualesquiera de sus vértices del eje focal.
) que existe entre su centro y cualesquiera de sus vértices del eje focal.La ecuacion queda:

Evidentemente esta operación se lleva a cabo en el conjunto de los números complejos.
Véase también: hipérbole
[editar] Historia
Ecuación de la hipérbola en su forma compleja
Una hipérbola en el plano complejo es el lugar geométrico formado por un conjunto de puntos
 , en el plano
, en el plano  ; tales que, cualesquiera de ellos satisface la condición geométrica de que el valor absoluto de la diferencia de sus distacias
; tales que, cualesquiera de ellos satisface la condición geométrica de que el valor absoluto de la diferencia de sus distacias 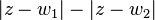 , a dos puntos fijos llamados focos
, a dos puntos fijos llamados focos y
y  , es una costante positiva igual al doble de la distancia (osea
, es una costante positiva igual al doble de la distancia (osea  ) que existe entre su centro y cualesquiera de sus vértices del eje focal.
) que existe entre su centro y cualesquiera de sus vértices del eje focal.La ecuacion queda:

Evidentemente esta operación se lleva a cabo en el conjunto de los números complejos.
Ecuaciones paramétricas
Hipérbola abierta de derecha a izquierda:
Imagen de sección cónica.
Una hipérbola es el lugar geométrico de los puntos de un plano tales que el valor absoluto de la diferencia de sus distancias a dos puntos fijos, llamados focos, es igual a la distancia entre los vértices, la cual es una constante positiva. |
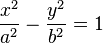
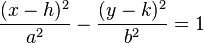

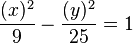



Luisa me gusto mucho tu blog esta muy bonito y muy lindo tu fondo
ResponderEliminarhuy luisa esta bonito tu blog pero no le pusiste entradas
ResponderEliminaresta buena la explicacion en tu blog pero le faltan las entradas
ResponderEliminar